Methodology
Decision Desk HQ is committed to providing accurate, reliable, and comprehensive poll averages that reflect the current state of public opinion, races for elective office, and ballot initiative efforts. Our methodology, detailed below, is designed to ensure that our poll averages are not only reflective of the latest data, but also methodologically sound and consistent over time.
Decision Desk HQ has averaged polls since the 2018 midterm election cycle, and over time, we've refined our methodology to focus on simplicity, interpretability, and accuracy. It's easy to get carried away with sophisticated statistical approaches that involve mining large amounts of historic polling data for every possible variable, but as has been shown over and over again, keeping it simple pays dividends when it comes to averaging polls.
Most approaches to averaging polls – though not ours – involve taking a base poll as presented from a vendor and then applying heavy alterations to the results. This typically includes work such as:
- Time weighting polls
- Adjusting polls for house effects and quality of polling
- Weighting different populations (e.g., likely voter, registered voter) differently
- Weighting by sample size
- Treating outliers
- After this, the results are typically averaged together using one of an array of methods, e.g., a moving average, exponentially weighted, or more complex approaches.
These approaches are all valid - but they also introduce a lot of subjective decisions about the exact way to treat certain types of data, and these decisions are sometimes made without having enough data to actually justify one decision over another.
Decision Desk HQ's goal is to provide a straightforward, consumer-facing average that accurately represents the state of available polls while being easy to interpret and not overly sensitive to recent news events. Once we've collected all the polls, we average the results using an adjusted cubic spline. A cubic spline is a third-degree piecewise polynomial function that allows for smooth interpolation between data points. It eliminates the possibility of any sudden deviation or break from earlier results.
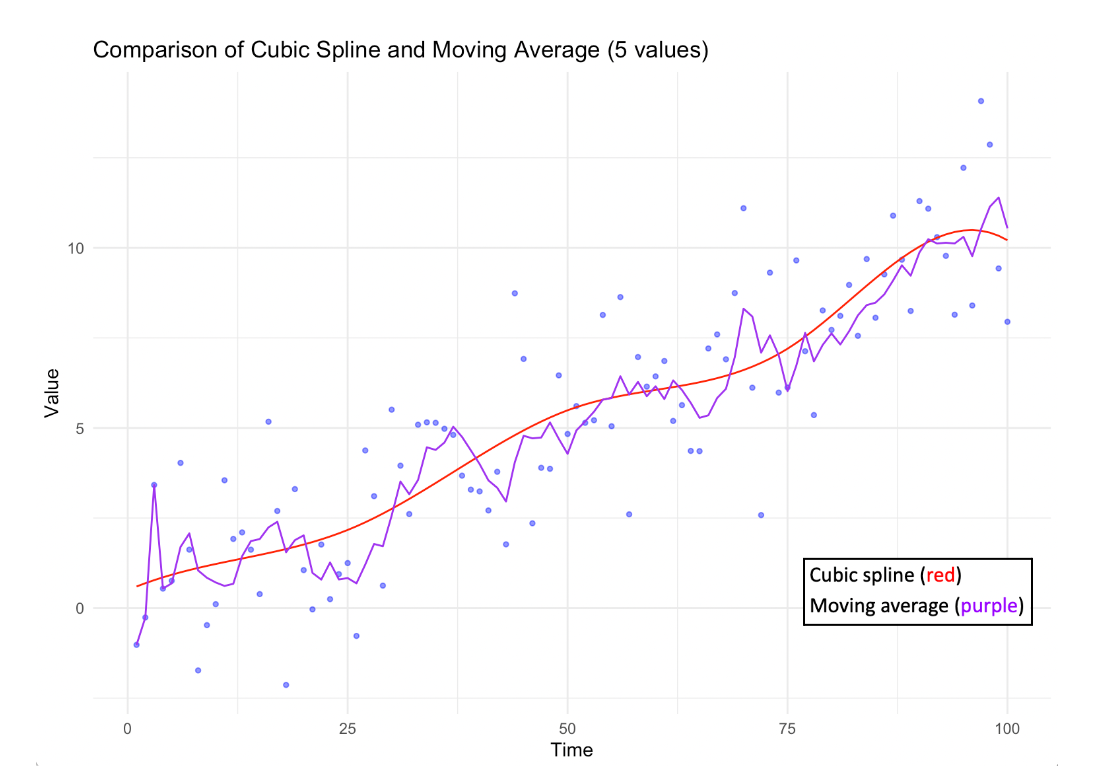
We fit a new spline every day, but will always retain results from previous days. Additionally, a minimum of five polls are required for us to publish an average for any race.
The advantages of this approach are that it refrains from what has become for many averages a borderline-forecasting function, while delivering results that are in-line with more sophisticated approaches. All publicly available polls will be included in the Decision Desk HQ polling database. We provide averages that capture as close to a complete picture of the electorate as possible.
Acknowledgement
Our poll average was created using polls sourced by Jayson Frascatore. The poll average methodology was designed by Patrick McCaul, and Matthew Rigby.